Transformer Implementation
This is the blog about the implementation of Transformer from Attention Is All You Need. The full code (model + training loop) is [here], which takes inspirations from [Reference].
Introduction
“Attention Is All You Need” (see [here]) is the original paper of the Transformer model, which is a powerful structure in the field of NLP and has been the foundation of many following works of different sub-fields of NLP. In this post, I will introduce the implementation of the Transformer in the following three steps: 1. the overall architecture of the Transformer; 2. the reusable components of the Transformer; 3. The final model constructed by the components from 2.
Overall Architecture
The following picture is from Attention Is All You Need and illustrates the overall architecture of the Transformer.
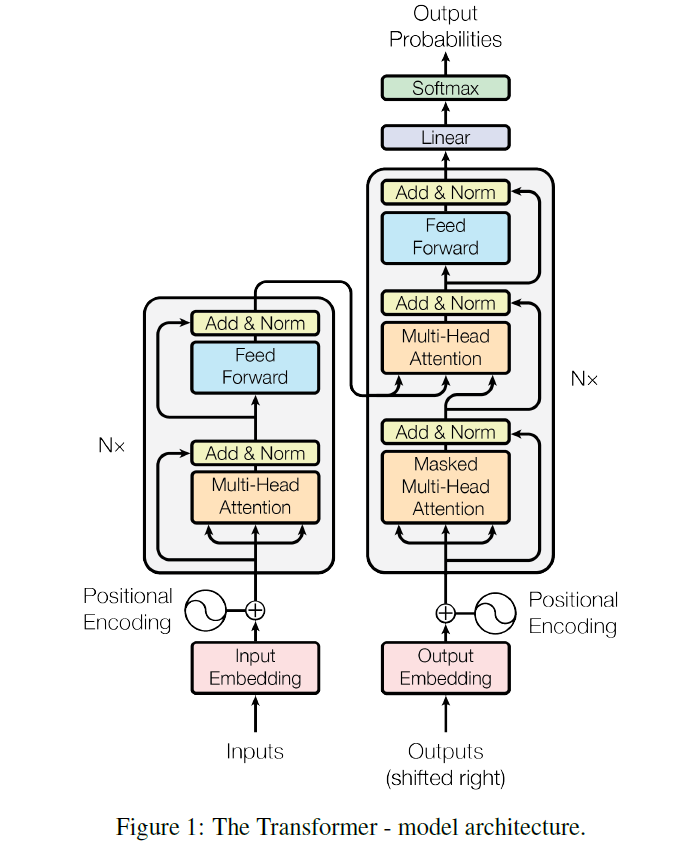
We can see that the Transformer is mainly composed of two parts: the Encoder and the Decoder. Both of which are then staked by N encoder/decoder blocks. And for each block, it can be decoupled into the following components: a. Multi-Head Attention; b. Add&Norm; c. Feed Forward. And there is an embedding module that embeds the discrete digits into neural-network-friendly dense vectors.
For an NLP task, given the source sequence $X=(BOS,\,x_1,\,…,x_n,\,EOS)$ and its target $Y=(BOS,\,y_1,\,…,y_m,\,EOS)$, the Transformer feeds $x$ as ‘inputs’ and embeds it into high-dimension dense vectors, which later are further encoded by the Encoder. When training, Target $y$ is shifted right (the last token $EOS$ is removed) and embedded to be fed into the Decoder as Outputs, where an interaction with the final outputs from the Encoder is performed in the Multi-Head Attention module. The final outputs from the Decoder are later projected to the target vocabulary size to produce the prediction $\hat{Y}=(\hat{y}_1,\,…,\hat{y}_m,\,EOS)$ When testing, at first there will only be $BOS$ fed into the Decoder to produce the first predicted token $\hat{y}_1$, and later $(BOS,\,\hat{y}_1)$ is fed and so on. (This process is called auto-regressive since the output from the last state is used as input for the current state.)
Components
As identified above, we have the following components that make up our Transformer model: a. Embedding; b. Multi-Head Attention; c. Add&Norm; d. Feed Forward.
a. Embedding
The Embedding has two parts: first is the embedding layer that maps discrete digits into dense vectors, and second is the positional encoding layer that gives the tokens $EOS,\,x_1,\,x_2,\,…$ in $X=(BOS,\,x_1,\,…,x_n,\,EOS)$ a sequential feature. (since unlike RNN taking one input token as a time, the Transformer takes inputs at one time)
import math
import torch
from torch import nn
class TransformerEmbedding(nn.Module):
def __init__(self, num_vocab, dim, dropout_rate, PAD, max_seq_len=5000, embedding_matrix=None, is_frozen=True):
super(TransformerEmbedding, self).__init__()
self.dim = dim
self.embedding = nn.Embedding(num_embeddings=num_vocab, embedding_dim=dim, padding_idx=PAD)
if embedding_matrix is not None:
assert embedding_matrix.size(0) != num_vocab or embedding_matrix.size(1) != dim
self.embedding.from_pretrained(embeddings=embedding_matrix, freeze=is_frozen)
self.dropout = nn.Dropout(dropout_rate)
self.register_buffer('PE', self.PositionalEncoding(max_seq_len=max_seq_len, dim=dim))
self.layer_norm = nn.LayerNorm(dim)
The above code is the “__init__” method of our Embedding. To be specific, it uses the nn.Embedding module to map discrete digits (0, 1, 2, …) into dense vectors of size “dim”. By passing “embedding_matrix” and “is_frozen” parameters, we can initialize the embedding table and decide whether it is trainable. We also can use the “self.register_buffer” method (inherited from “nn.Module”, and can be quickly accessed as a constant) to store the positional encoding, which is computed by:
The above formula tells us for a token at position $pos$ in a sequence, the positional encoding of its even dimension is a $sin$ function and that of odd dimension is a $cos$ function. The wavelength for dimension $2i$ and $2i+1$ is $2\pi·10000^{2i\,/d_{model}}\in[2\pi,\,10000·2\pi]$ and the max length that positional encoding can present is roughly viewed as $10000$ (since the max period is $10000·2\pi$). One good thing about using trigonometric functions is: $sin(pos+k)=sin(pos)cos(k)+cos(pos)sin(k)$ and $cos(pos+k)=cos(pos)cos(k)-sin(pos)sin(k)$; thus, the relationship between the $pos$-th position and $pos+k$-th position in the sentence can be view as a linear transformation $PE_{pos}\longrightarrow PE_{pos+k}$ where the coefficients are constants about $k$, namely, $sin(w_i·k)$ and $cos(w_i·k)$ (see discussion [here]).
The implementation is:
@staticmethod
def PositionalEncoding(max_seq_len, dim):
pe = torch.zeros((max_seq_len, dim))
position = torch.arange(0, max_seq_len).unsqueeze(1)
# returns: value: [0, 1, ..., max_seq_len-1] ; shape: (max_seq_len, 1)
div_term = torch.exp(-torch.arange(0, dim, 2) / dim * math.log(10000.0))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
# i:j:k means from position i to j, take indices every k steps.
return pe
where noticing the div_term is actually:
\[\frac{1}{10000^{2i/d_{model}}}=e^{log(\frac{1}{10000^{2i/d_{model}}})}=e^{-\frac{2i}{d_{model}}log10000}\]And we can defined the computation process as:
def forward(self, inputs):
# inputs shape: (batch_size, seq_len)
seq_len = inputs.size(1)
return self.layer_norm(self.dropout(self.embedding(inputs) * math.sqrt(self.dim)+self.PE[:seq_len]))
Note that after “self.embedding(inputs)” it is multiplied by $\sqrt{d_{model}}$ (which is the case in [2] and [3]) and a layer normalization is performed before output. (which is as well equivalent to the implementations from [2] and [3]). In [1], the returning is simply: self.dropout(self.embedding(inputs) + self.PE[:seq_len])
b. Multi-Head Attention
The Attention layer follows the following computation operation: $Attention(Q,\,K,\,V)=softmax(\frac{Q·K^{T}}{\sqrt{d_k}})·V$, and the term “Multi-Head” can be roughly treated as performing this operation multiple times for the same set of $Q,\,K,\,V$. To be specific, the Multi-Head Attention is computed by:
The implementation is:
import math
import torch
from torch import nn
from torch.nn import functional as F
class Attention(nn.Module):
def __init__(self, dim, num_heads, dropout_rate=None):
super(Attention, self).__init__()
assert dim % num_heads == 0
self.num_heads = num_heads
self.sub_dim = dim // num_heads
self.W_K = nn.Linear(in_features=dim, out_features=dim)
self.W_Q = nn.Linear(in_features=dim, out_features=dim)
self.W_V = nn.Linear(in_features=dim, out_features=dim)
self.W_out = nn.Linear(in_features=dim, out_features=dim)
self.dropout_rate = dropout_rate
if dropout_rate is not None:
self.dropout = nn.Dropout(dropout_rate)
The “__init__” method of our Multi-Head Attention layer is quite simple. By passing the number of attention heads, we are actually operating on the hidden dimension (split it into num_heads equal parts) to do the attention. Note for Multi-Head Attention the module “nn.Dropout” is not in [1] and can be turned off in [2] and [3].
The forward pass of out attention layer will be:
def forward(self, Q, K, V, mask=None):
# inputs is of shape (batch_size, seq_len, dim)
batch_size = Q.size(0)
Q = self.W_Q(Q).view(batch_size, Q.size(1), self.num_heads, self.sub_dim).transpose(1, 2)
# shape: (batch_size, seq_len, num_heads, sub_dim) ---> (batch_size, num_heads, seq_len_q, sub_dim)
K = self.W_K(K).view(batch_size, K.size(1), self.num_heads, self.sub_dim).transpose(1, 2)
# shape: (batch_size, num_heads, seq_len_kv, sub_dim)
V = self.W_V(V).view(batch_size, V.size(1), self.num_heads, self.sub_dim).transpose(1, 2)
# shape: (batch_size, num_heads, seq_len_kv, sub_dim)
att_score = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.sub_dim)
if mask is not None:
att_score = att_score.masked_fill(mask, -1e9)
att_score = F.softmax(att_score, dim=-1)
# (batch_size, num_heads, seq_len_q, seq_len_kv)
if mask is not None:
att_score = att_score.masked_fill(mask, 0)
if self.dropout_rate is not None:
att_score = self.dropout(att_score)
outputs = torch.matmul(att_score, V).transpose(1, 2).contiguous().view(
batch_size, -1, self.num_heads * self.sub_dim)
# shape: (batch_size, num_heads, seq_len_q, sub_dim) ---> (batch_size, seq_len_q, num_heads, sub_dim)
return self.W_out(outputs)
# shape: (batch_size, seq_len_q, dim)
We can see that, for a given input, say Q, a following pre-processing is performed:
\[(batch\_size,\,seq\_len\_q,\,dim\stackrel{W^{Q}}{\longrightarrow}dim)\stackrel{reshape}{\longrightarrow}(batch\_size,\,num\_heads,\,seq\_len\_q,\,sub\_dim)\]And the “Multi-Head” operation is actually performed by one matrix (in our example: $W^Q$). The following codes are quite easy to understand. Note that [1], [2], [3] all implement the $Attention(Q,\,K,\,V)=softmax(\frac{Q·K^{T}}{\sqrt{d_k}})·V$ as another callable function (such as “def attention(query, key, value, mask=None, dropout=None):”) and masking the padded positions of attention score “att_score = att_score.masked_fill(mask, 0)” is not in [2] and [3]. And the usage of “.reshape()”, “.view()”, and “.contiguous()” is specified [here]
A very important thing is the shape of the mask. Based on the function of the masks, we can simply divide them into two kinds: padding mask (used in Multi-Head Attention, both in the Encoder and the Decoder, see [overall architecture]) and subsequent mask (used in Masked Multi-Head Attention, only in the Decoder, see [overall architecture]). A padded mask is to mask out the paddings in the sentence, for example: for an input: $[3,\,5,\,8,\,9,\,4,\,0,\,0,\,0]$, the three zeros at the end are just place holders thus should not be considered real words. A subsequent mask , however is only used in the decoder, and is of shape: $seq\_len\_outputs\times seq\_len\_outputs$ where $seq\_len\_outputs$ is the sentence length of the “Outputs” fed into the Decoder (see [overall architecture]). A general sense of the subsequent mask is this ($seq\_len\_outputs=3$):
where the diagonal and below are all set to 0 (or 1) and above the diagonal are all set to 1 (or 0).
c. Add&Norm
This layer simply leverages the residual connection from [paper] to add a direct path between two sub-layers to avoid gradient vanishing, which can be implemented by: $LayerNorm(x+Sublayer(x))$ where $x$ is the input of the sub-layer and $Sublayer(x)$ is its output.
# This is the example from the encoder block
inputs = self.layer_norm(inputs + self.att(inputs, inputs, inputs, pad_mask))
# att: Q=inputs, K=inputs, V=inputs
return self.layer_norm(inputs + self.dropout(self.feedforward(inputs)))
# This is the example from the decoder block
inputs = self.layer_norm(inputs + self.masked_att(inputs, inputs, inputs, upper_triangle_mask))
# masked_att: Q=inputs, K=inputs, V=inputs, mask=upper_triangle_mask
inputs = self.layer_norm(inputs + self.att(inputs, encoder_outputs, encoder_outputs, pad_mask))
# att: Q=inputs, K=encoder_outputs, V=encoder_outputs, mask=pad_mask
return self.layer_norm(inputs + self.dropout(self.feedforward(inputs)))
d. Feed Forward
The full name of this layer is called Position-wise Feed-Forward Networks in the origin paper, since it’s applied to each position separately. And it is computed by:
\[FFN(x)=max(0,\,xW_1+b_1)W_2+b_2\]The implementation is very simple:
import torch
from torch import nn
from torch.nn import functional as F
# implements: max(0, x·W_1 + b_1)·W_2 + b_2
class FeedForward(nn.Module):
def __init__(self, dim, inner_layer_dim, dropout_rate): # in paper: dim=512, inner_layer_dim=2048
super(FeedForward, self).__init__()
self.W_1 = nn.Linear(in_features=dim, out_features=inner_layer_dim)
self.W_2 = nn.Linear(in_features=inner_layer_dim, out_features=dim)
self.dropout = nn.Dropout(dropout_rate)
def forward(self, inputs):
return self.W_2(self.dropout(F.relu(self.W_1(inputs))))
Final Model
With the aforementioned four basic components, we can now build our Transformer model! First, we need to construct the encoder/decoder block for the Encoder/Decoder, and then aggregate them together to get our final model. At last, we will also look a little deeper into the decoding strategies when testing.
A encoder block is:
from torch import nn
from copy import deepcopy
class TransformerBaseEncoderBlock(nn.Module):
# the input is of size: (batch_size, seq_len, dim)
def __init__(self, dim, dropout_rate, Attention, FeedForward):
super(TransformerBaseEncoderBlock, self).__init__()
self.att = deepcopy(Attention)
# for reusable components, we pass it in as parameter and use deepcopy()
self.layer_norm = nn.LayerNorm(normalized_shape=dim)
# normalized_shape:
# If a single integer is used, it is treated as a singleton list, and this module will normalize over the last
# dimension which is expected to be of that specific size.
self.feedforward = deepcopy(FeedForward)
self.dropout = nn.Dropout(dropout_rate)
def forward(self, inputs, pad_mask):
inputs = self.layer_norm(inputs + self.att(inputs, inputs, inputs, pad_mask))
# att: Q=inputs, K=inputs, V=inputs
return self.layer_norm(inputs + self.dropout(self.feedforward(inputs)))
where the modules (such as Attention, FeedForward) are the components you see from the previous section. And by stacking these blocks together, we can get the Encoder:
class TransformerBaseEncoder(nn.Module):
def __init__(self, num_encoder_block, encoder_block):
super(TransformerBaseEncoder, self).__init__()
self.encoder_blocks = nn.ModuleList([deepcopy(encoder_block) for _ in range(num_encoder_block)])
# nn.ModuleList receives a list containing modules and stores them
def forward(self, inputs, mask):
# inputs are the embedded source sentences
for block in self.encoder_blocks:
inputs = block(inputs, mask)
return inputs
where the encoder_block is the above-defined TransformerBaseEncoderBlock module, and by calling its “forward()” method, we can get the final output of the entire Transformer encoder.
Similarly, a decoder block is defined as:
from torch import nn
from copy import deepcopy
class TransformerBaseDecoderBlock(nn.Module):
def __init__(self, dim, dropout_rate, Attention, FeedForward):
super(TransformerBaseDecoderBlock, self).__init__()
self.masked_att = deepcopy(Attention)
self.att = deepcopy(Attention)
self.layer_norm = nn.LayerNorm(normalized_shape=dim)
self.feedforward = deepcopy(FeedForward)
self.dropout = nn.Dropout(dropout_rate)
def forward(self, encoder_outputs, inputs, pad_mask, upper_triangle_mask):
inputs = self.layer_norm(inputs + self.masked_att(inputs, inputs, inputs, upper_triangle_mask))
# masked_att: Q=inputs, K=inputs, V=inputs, mask=upper_triangle_mask
inputs = self.layer_norm(inputs + self.att(inputs, encoder_outputs, encoder_outputs, pad_mask))
# att: Q=inputs, K=encoder_outputs, V=encoder_outputs, mask=pad_mask
return self.layer_norm(inputs + self.dropout(self.feedforward(inputs)))
And the Decoder is then implemented as:
class TransformerBaseDecoder(nn.Module):
def __init__(self, num_decoder_block, decoder_block):
super(TransformerBaseDecoder, self).__init__()
self.decoder_blocks = nn.ModuleList([deepcopy(decoder_block) for _ in range(num_decoder_block)])
def forward(self, encoder_outputs, inputs, pad_mask, upper_triangle_mask):
# inputs are the embedded target sentences (training) / the newest embedded decoded word (test)
for decoder_block in self.decoder_blocks:
inputs = decoder_block(encoder_outputs, inputs, pad_mask, upper_triangle_mask)
return inputs
where the decoder_block is just the above-defined TransformerBaseDecoderBlock
Finally, we can define our Transformer as:
import torch
from torch import nn
from torch.nn import functional as F
from model.Embedding import TransformerEmbedding
from model.Attention import Attention
from model.FeedForward import FeedForward
from model.TransformerEncoder import TransformerBaseEncoderBlock, TransformerBaseEncoder
from model.TransformerDecoder import TransformerBaseDecoderBlock, TransformerBaseDecoder
class TransformerBase(nn.Module):
def __init__(self, num_encoder_block, num_decoder_block, num_heads, num_vocab_src, num_vocab_tgt,
dim, inner_layer_dim, dropout_rate, PAD, BOS, EOS):
super(TransformerBase, self).__init__()
self.PAD = PAD
self.BOS = BOS
self.EOS = EOS
self.num_vocab_tgt = num_vocab_tgt
attention = Attention(dim=dim, num_heads=num_heads)
feedforward = FeedForward(dim=dim, inner_layer_dim=inner_layer_dim, dropout_rate=dropout_rate)
encoder_block = TransformerBaseEncoderBlock(dim=dim, dropout_rate=dropout_rate, Attention=attention,
FeedForward=feedforward)
decoder_block = TransformerBaseDecoderBlock(dim=dim, dropout_rate=dropout_rate, Attention=attention,
FeedForward=feedforward)
self.embedding_src = TransformerEmbedding(num_vocab=num_vocab_src, dim=dim, dropout_rate=dropout_rate, PAD=PAD)
self.embedding_tgt = TransformerEmbedding(num_vocab=num_vocab_tgt, dim=dim, dropout_rate=dropout_rate, PAD=PAD)
self.encoder = TransformerBaseEncoder(num_encoder_block=num_encoder_block, encoder_block=encoder_block)
self.decoder = TransformerBaseDecoder(num_decoder_block=num_decoder_block, decoder_block=decoder_block)
self.projection = nn.Linear(in_features=dim, out_features=num_vocab_tgt)
The main components in our Transformer are: embedding layers of the source (inputs) and target (outputs); the Encoder and the Decoder; a projection layer $\mathbf{R}^{dim}\longrightarrow \mathbf{R}^{target\,vocab} $ that maps the final output to the vocabulary of the target.
Note that in [2] and [3] there are two embedding layers for source and target respectively. In [1] there is only one embedding layer shared for source and target.
Before we define the forward pass of our model, let’s first met some masking functions that helps us:
def create_pad_mask(self, x):
return (x == self.PAD).to(x.device)
# padded places are True, real words are False
@staticmethod
def create_upper_triangle_mask(x):
seq_len = x.size(-1) # x shape: (batch_size, seq_len)
return torch.ones((seq_len, seq_len)).triu(1).bool().to(x.device)
# unseen words are True, available words are False
The above two functions produce the aforementioned two different kinds of masks, namely [padded mask] and [subsequent mask]. And now we define the forward pass of our model as:
# inputs shape: (batch_size, seq_len)
def forward(self, inputs, targets):
inputs_mask = self.create_pad_mask(inputs).unsqueeze(1).unsqueeze(2)
# of shape: (batch_size, 1, 1, seq_len_inputs) <---> in Attention,
# when masking, (Q·K.transpose) is of shape: (batch_size, num_heads, seq_len_q, seq_len_kv)
# where the seq_len_kv should equal inputs' seq_len
inputs = self.embedding_src(inputs)
from_encoder = self.encoder(inputs, inputs_mask)
# shape: (batch_size, seq_len, dim)
outputs = self.teacher_forcing(inputs_mask=inputs_mask, from_encoder=from_encoder, targets=targets)
return outputs
# the outputs are the log probabilities of shape: (batch_size, seq_len, vocab)
def teacher_forcing(self, inputs_mask, from_encoder, targets):
pad_mask = self.create_pad_mask(targets).unsqueeze(1)
upper_triangle_mask = self.create_upper_triangle_mask(targets).unsqueeze(0)
upper_triangle_mask = upper_triangle_mask + pad_mask # batch_size, seq_len, seq_len
# now the dtype is int, should convert to bool later
# the upper_triangle_mask should not only mask the unseen words but also the paddings
targets = self.embedding_tgt(targets)
outputs = self.decoder(from_encoder, targets, inputs_mask, upper_triangle_mask.unsqueeze(1).bool())
outputs = F.log_softmax(self.projection(outputs), dim=-1)
# shape: (batch_size, seq_len, dim ---> vocab)
return outputs
During training the Transformer adapts the teacher-forcing training strategy, which means the decoder at time-step $t$ will always be fed the ground truth output token $y_t$ instead of using its own prediction $\hat{y}_t$ from time-step $t-1$. Another interesting observation is that the final output is not the probabilities but the log of them. (since F.log_softmax() is used instead of F.softmax()) This is because for loss computing we use the “nn.KLDivLoss”, which expects the predictions to be log probabilities. Finally we need to talk about the masks used here: a. the padded mask for the Encoder is used to mask the paddings in the inputs; b. the subsequent mask used in the Decoder is a little bit different from what we discussed [here], it is actually the combination of a standard subsequent mask and a padded mask, which function is not only to prevent from attending to future tokens ($y_{t+1},\,y_{t+2},\,…$) at time-step $t$ but also to mask out the paddings; c. in [2] and [3] the padded mask in the Decoder is used for masking the paddings in source (input, which serves as K in Multi-Head Attention), however that of [1] is used for masking the paddings in targets (outputs, which serves as Q in Multi-Head Attention), and here I follow the implementation of [2] and [3].
At last, we now introduce implementation of the inference:
def predict(self, inputs, max_generating_len=512, decoding_method='greedy', beam_size=5):
inputs_mask = self.create_pad_mask(inputs).unsqueeze(1).unsqueeze(2)
inputs = self.embedding_src(inputs)
from_encoder = self.encoder(inputs, inputs_mask)
sentences = self.greedy(inputs_mask=inputs_mask, from_encoder=from_encoder, max_generating_len=max_generating_len) \
if decoding_method == 'greedy' else \
self.beam_search(from_encoder=from_encoder, max_generating_len=max_generating_len, beam_size=beam_size)
return sentences
for the decoding methods (“greedy” and “beam_search”), I did a minor adjustment to the decoding methods provided in [1] (basically the same, and it is already very excellent in [1]). And here I just introduce the idea of implementations for these two methods.
For “greedy”:

For “beam search”:

Reference
The following projects/websites are used as code references:
[1] SDISS is a Transformer-based sentence simplification model
[2] The Annotated Transformer is a post about the Transformer and its implementation
[3] How to code The Transformer in Pytorch is a post about the Transformer and its implementation
Enjoy Reading This Article?
Here are some more articles you might like to read next: